目录
一、学习内容
二、matlab基本知识
三、线性点运算
四、非线性点运算,伽马矫正
五、直方图
1、直方图均衡化
(1)使用histep函数实现图像均衡化
(2)使用自行编写的均衡化函数实现图像均衡化
2、直方图规定化
(1)使用histep函数实现图像均衡化
(2)使用自行编写的规定化函数实现图像规定化
六、平滑滤波器
1、T3
(1)图像平滑:
(2)图像增强:
2、中值滤波
3、高斯滤波
七、Sobel算子、Prewitt算子、Roberts算子和LoG滤波器
1、Sobel算子
2、Prewitt算子
3、Roberts算子
4、LoG滤波器
5、几种算子的比较
一、学习内容
1、学习使用点运算,非线性点运算,伽马矫正处理图像
2、利用histeg函数,实现直方图规定化
3、不使用histeq函数,自行编写直方图均衡化函数,并用于图像处理
4、学习使用平滑滤波器: 、高斯滤波处理图像
5、学习使用Sobel算子、Prewitt算子、Roberts算子和LoG算子
二、matlab基本知识
1、常用函数
imread:读取图像,
imshow:显示图像
rgb2gray:彩色图像转换为灰度图像
figure:创建窗口
subplot:单个窗口绘制多个图像
2、%%使得代码分块运行,%用于注释
3、安装路径下的:toolbox\images\imdata带有matlab自带的图像,可直接使用(文末有本文章使用的全部图像,可自行下载)
4、命令框:doc 函数名 可以跳转官方说明文档,查看函数使用
5、函数定义需要放在代码后,函数支持多个返回值
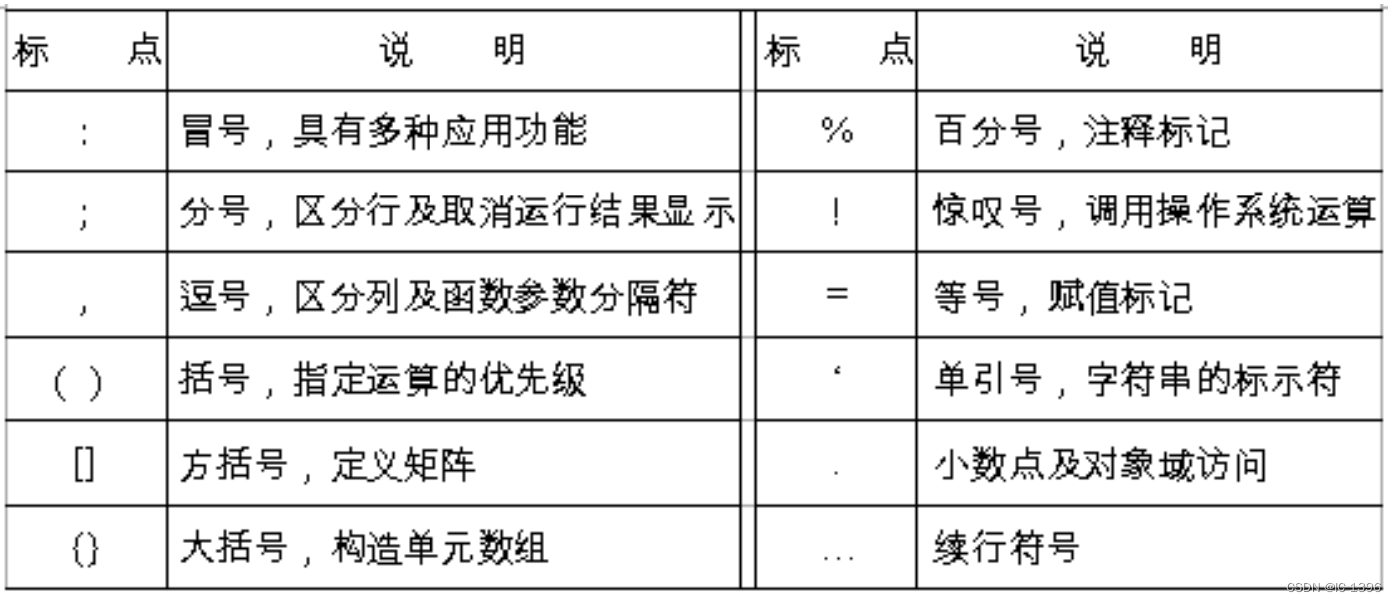
6、常用命令和符号
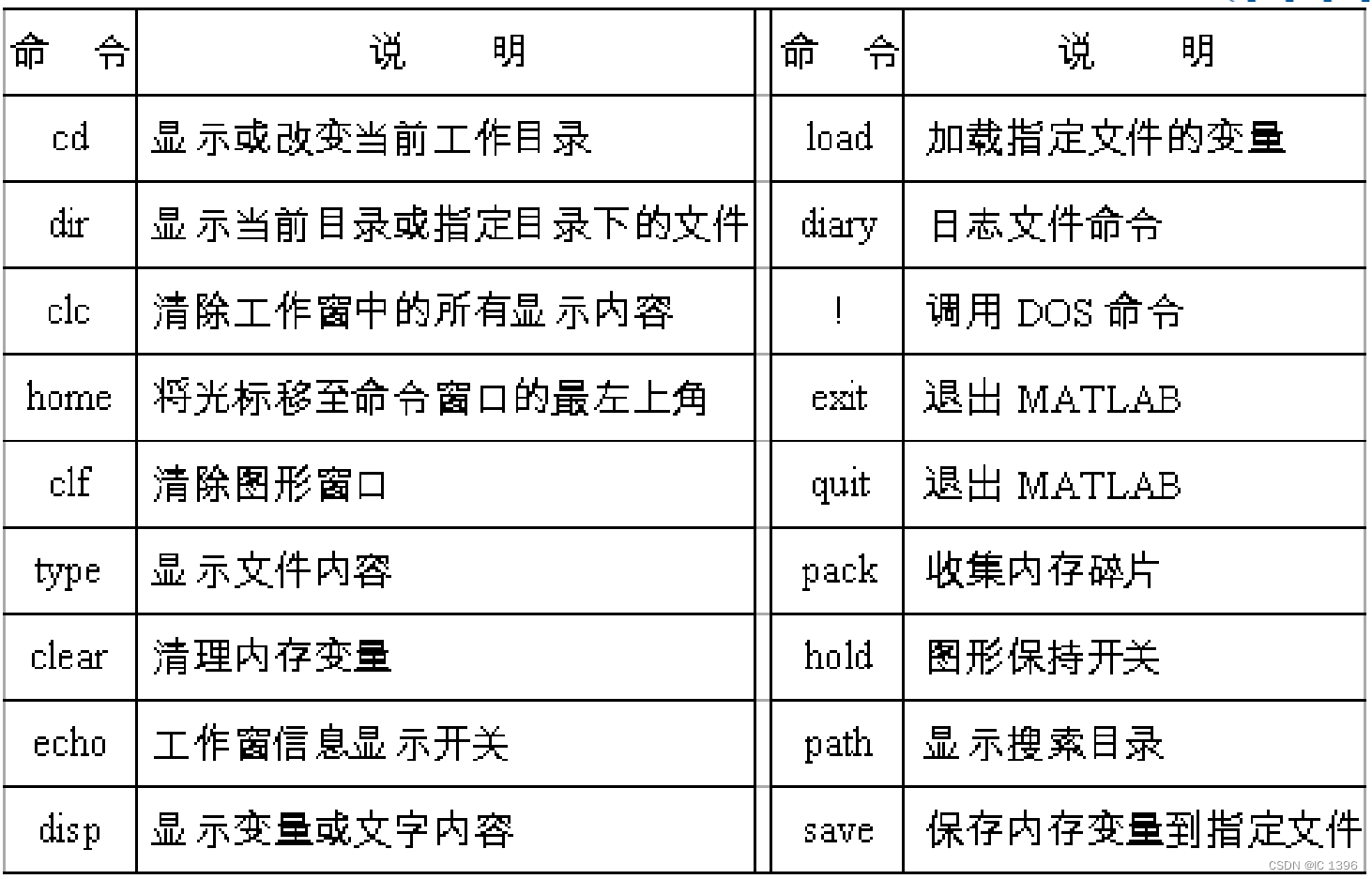
三、线性点运算
数字图像数据是以矩阵形式存放的,矩阵的每个元素对应着一个像素点的像素值。点运算又称对比增强、对比拉升或灰度变换,通过图像中的每一个像素值进行运算的图像处理方式,其运算结果不会改变图像内像素点之间的空间关系,常用于改变图像的灰度范围及分布,
其运算的数学关系式为:
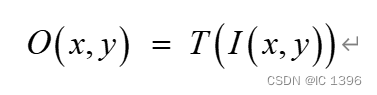
I(x,y)—原图像
O(x,y)—经过点运算处理后的图像
T—点运算的关系函数
线性点运算的灰度变换函数形式可以采用线性方程描述,即o(x,y) = a*I(x,y)+ b,即通过数乘及加法改变图像的灰度范围及分布,使用点运算需要注意结果不能超过限定值,否则将导致图片过曝或者损失暗部细节
-
%%
-
% 点运算,实现图像对比度的改变
-
clc;clear;close all; % 初始化
-
Image1=imread(strip(input(‘请输入照片路径(图片右键复制文件地址即可):’,’s’),'”‘)); % 读入一幅图像
-
Image1=im2double(Image1); % 转换数据类型为double
-
subplot(231);imshow(Image1);title(‘原图’);
-
% 增加对比度并显示
-
a=2;b=-50; % 增加对比度
-
O=a.*Image1+b/255;
-
subplot(232);imshow(O);title(‘a=2;b=-50,增加对比度’);
-
-
% 降低对比度并显示
-
a=0.5;b=-50; %降低对比度
-
O=a.*Image1+b/255;
-
subplot(233);imshow(O);title(‘a=0.5;b=-50,降低对比度’);
-
-
% 线性增加亮度
-
a=1;b=50;
-
O=a.*Image1+b/255;
-
subplot(234);imshow(O);title(‘a=1;b=50,线性平移增加亮度’);
-
-
% 线性降低亮度
-
a=1;b=-50;
-
O=a.*Image1+b/255;
-
subplot(235);imshow(O);title(‘a=1;b=-50,线性平移降低亮度’);
-
-
% 图像反色
-
a=-1;b=255;
-
O=a.*Image1+b/255;
-
subplot(236);imshow(O);title(‘a=-1;b=255,图像反色’);



对比色环可以发现:
① b一定,a越大,对比度增加,越明亮
② a一定,b越大,越明亮,但是对比度不变,颜色向着色环中心靠近
③ a=-1,b=255时,颜色取反,即在色环中变成中心对称的颜色,像黄色变成蓝色
四、非线性点运算,伽马矫正
当处理后的图像各个像素点不与原图像成线性关系时,即为非线性点运算
常用的非线性点运算有伽马矫正(Gamma Correction),他是一种图像或视频处理技术,它可以使人眼看到的颜色更加精确和鲜艳。
其运算的数学关系式为:
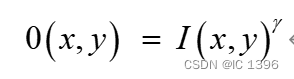
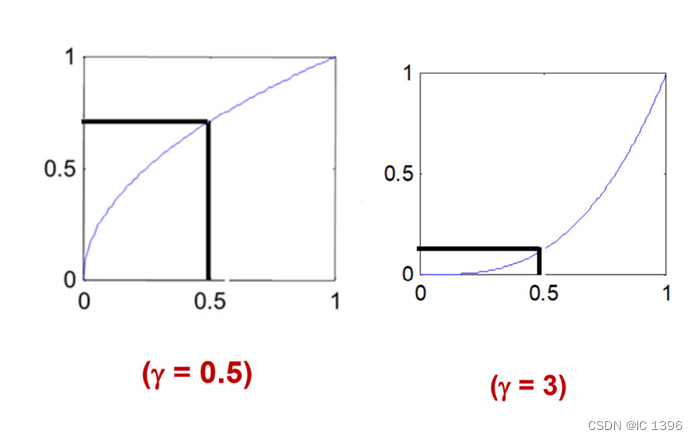
伽马值γ < 1的情况有时被称作编码伽马值, 也叫伽马压缩。低灰度值区域动态范围变大,增强灰暗区域的对比度,图像整体灰度值变大;
伽马值γ > 1的情况有时也被称作解码伽马值,也叫伽马展开。高灰度值区域动态范围变大,增强明亮区域的对比度,图像整体灰度值变小。
-
%%
-
%伽马矫正
-
clc
-
Image1=imread(strip(input(‘请输入照片路径(图片右键复制文件地址即可):’,’s’),'”‘));
-
Image1 = rgb2gray(Image1);
-
Image2 = imadjust(Image1,[],[],2);
-
Image3 = imadjust(Image1,[],[],1);
-
Image4 = imadjust(Image1,[],[],0.5);
-
-
figure,
-
subplot(241),imshow(Image1),title(‘原图’);
-
subplot(242),imshow(Image2),title(‘Gamma 2’);
-
subplot(243),imshow(Image3),title(‘Gamma 1’);
-
subplot(244),imshow(Image4),title(‘Gamma 0.5’);
-
subplot(245),imhist(Image1),title(‘原图直方图’);
-
subplot(246),imhist(Image2),title(‘Gamma 2 直方图’);
-
subplot(247),imhist(Image3),title(‘Gamma 1 直方图’);
-
subplot(248),imhist(Image4),title(‘Gamma 0.5 直方图’);


伽马值γ=0.5,低灰度值区域动态范围变大,增强灰暗区域的对比度,图像整体灰度值变大;伽马值γ=1时图像与原先一致;伽马值γ=2时高灰度值区域动态范围变大,增强明亮区域的对比度,图像整体灰度值变小。
五、直方图
图片直方图是一种用于表示数字图像亮度分布的图表,由一系列相邻区间组成的垂直条形图,每个区间代表了一个亮度范围,并给出该亮度范围内像素数量的计数。横轴表示亮度值的范围,纵轴表示该亮度值范围内像素的数量。直方图可以用来分析图像的亮度、对比度、色彩平衡等特征。
1、直方图均衡化
直方图均衡(Histogram Equalization)是一种图像处理技术,它可以通过重新分配图像像素的亮度值来增强图像的对比度和清晰度,从而改善图像的质量。在直方图均衡化技术中,算法的主要目标是对输入图像的亮度分布进行变换,使其均匀分布在整个亮度范围内,从而使图像的亮度值空间更加合理,增强图像的明暗效果。
直方图均衡化的过程如下:

直方图均衡化在图像增强、图像分割、运动检测、图像配准等领域有着广泛的应用。需要注意的是,在一些情况下,直方图均衡化可能会导致图像细节的丢失和不自然的效果,因此在使用该技术时应根据实际情况选择是否合适。
(1)使用histep函数实现图像均衡化
注:里面同时包含了使用histep实现图像规定化,可在看完图像规定化后返回阅读
-
%%
-
%直方图均衡化,规定化
-
clc;clear;close all;
-
-
%读入文件文件
-
Image1 = rgb2gray(imread(strip(input(‘请输入lena路径(图片右键复制文件地址即可):’,’s’),'”‘)));%读取图像并灰度化
-
Image2 = imread(strip(input(‘请输入coins路径(图片右键复制文件地址即可):’,’s’),'”‘));%读取coins图片
-
Image3 = imread(strip(input(‘请输入circuit路径(图片右键复制文件地址即可):’,’s’),'”‘));%读取circuit图片
-
Image4 = imread(strip(input(‘请输入cameraman路径(图片右键复制文件地址即可):’,’s’),'”‘));%读取cameraman图片
-
-
%获取直方图
-
Hgram2 = imhist(Image2);%获取直方图
-
Hgram3 = imhist(Image3);
-
Hgram4 = imhist(Image4);
-
-
%histeq函数实现直方图的均衡化和规定化
-
result1 = histeq(Image1); %直方图均衡化
-
result2 = histeq(Image1,Hgram2); %直方图的规定化到coins
-
result3 = histeq(Image1,Hgram3); %直方图的规定化到circuit
-
result4 = histeq(Image1,Hgram4); %直方图的规定化到cameraman
-
-
subplot(221),imshow(Image1),title(‘原图’);
-
subplot(222),imshow(result1),title(‘直方图均衡化’);
-
subplot(223),imhist(Image1),title(‘原图直方图’);
-
subplot(224),imhist(result1),title(‘均衡化之后的图像的直方图’);
-
-
figure,
-
subplot(231),imshow(Image1),title(‘原图’);
-
subplot(232),imshow(Image2),title(‘目标图’);
-
subplot(234),imhist(Image1),title(‘原图直方图’);
-
subplot(235),imhist(Image2),title(‘目标图直方图’);
-
subplot(233),imshow(result2),title(‘直方图的规定化到coins’);
-
subplot(236),imhist(result2),title(‘规定化之后图像的直方图’);
-
-
-
figure,
-
subplot(231),imshow(Image1),title(‘原图’);
-
subplot(232),imshow(Image3),title(‘目标图’);
-
subplot(234),imhist(Image1),title(‘原图直方图’);
-
subplot(235),imhist(Image3),title(‘目标图直方图’);
-
subplot(233),imshow(result3),title(‘直方图的规定化到circuit’);
-
subplot(236),imhist(result3),title(‘规定化之后图像的直方图’);
-
-
figure,
-
subplot(231),imshow(Image1),title(‘原图’);
-
subplot(232),imshow(Image4),title(‘目标图’);
-
subplot(234),imhist(Image1),title(‘原图直方图’);
-
subplot(235),imhist(Image4),title(‘目标图直方图’);
-
subplot(233),imshow(result4),title(‘直方图的规定化到cameraman’);
-
subplot(236),imhist(result4),title(‘规定化之后图像的直方图’);


由图像可以看到,经过均衡化后,图像的直方图分布变均匀,对比度下降,形成灰度级分布概率均衡的图像。
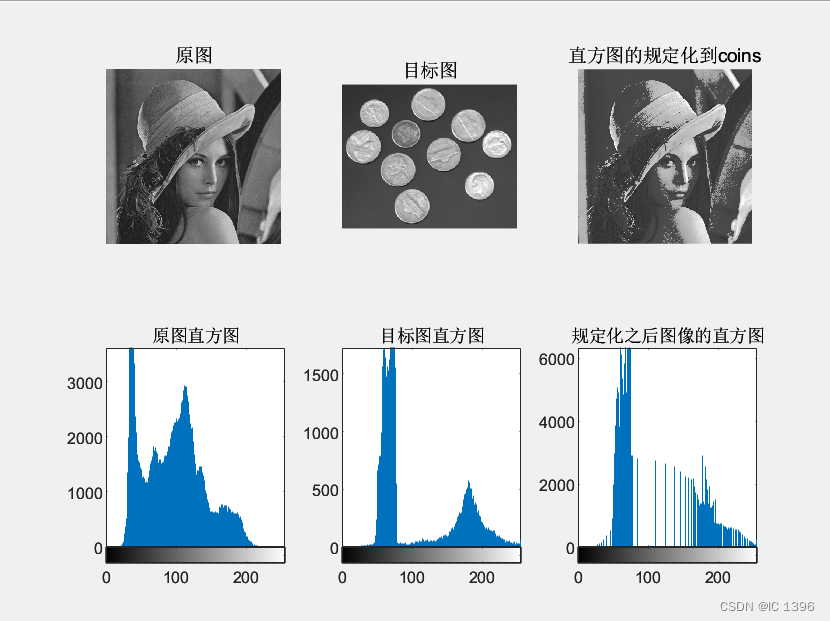
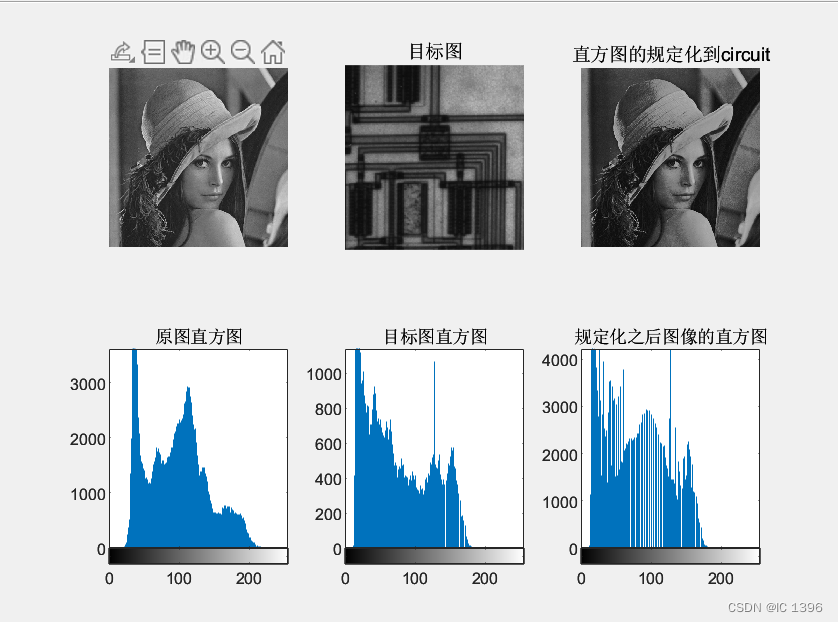
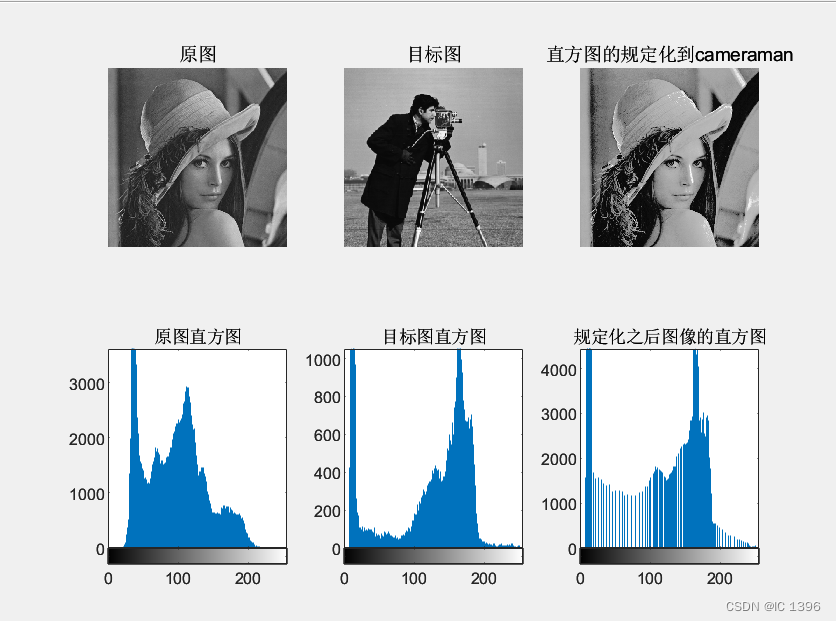
经过规定化后,图像的灰度级分布分布与规定化的分布规律相同
(2)使用自行编写的均衡化函数实现图像均衡化
-
%%
-
% 不使用histep函数实现均衡化
-
clc
-
Image1=imread(strip(input(‘请输入照片路径(图片右键复制文件地址即可):’,’s’),'”‘)); %读取图像
-
%判断是否为灰度图像
-
mysize=size(Image1);
-
if numel(mysize)>2 %若维度大于2
-
Image1=rgb2gray(Image1); %将彩色图像转换为灰度图像
-
end
-
-
result1 = hist_1(Image1);%调用函数均衡化
-
-
result2 = histeq(Image1);
-
-
figure,
-
subplot(231),imshow(Image1),title(‘原图’);
-
subplot(234),imhist(Image1),title(‘原图直方图’);
-
subplot(232),imshow(result1),title(‘自行编写直方图均衡化’);
-
subplot(235),imhist(result1),title(‘自行编写均衡化直方图’);
-
subplot(233),imshow(result2),title(‘内置直方图均衡化’);
-
subplot(236),imhist(result2),title(‘使用内置均衡化直方图’);
-
-
%%
-
%函数部分,均衡化函数
-
function hist_img = hist_1(I)
-
[R, C] = size(I);%获取图片行列像素点个数
-
img_size = R*C;%得总像素点
-
c = zeros(1,256);%返回1*256一维数组,元素均为0,用于统计每个像素值的个数
-
b= c;%存档,用于转化前后的对照表
-
%Max1=max(max(I))
-
%Min1=min(min(I))
-
-
temp = I(:);
-
temp = sort(temp);%像素点灰度值排序
-
-
for i = 1:img_size %遍历全部像素点
-
c(temp(i)+1) = c(temp(i)+1)+1; %索引c中对应的temp(i)+1位加1,temp为灰度值
-
end
-
%若引入累积分布函数最小值cdfmin时,不需要执行c=c/img_size;
-
c=c/img_size;
-
a = c;
-
-
for i = 2:256 %求和,得到累积分布函数
-
a(i) = c(i) + a(i-1);
-
end
-
-
-
%根据直方图均衡化算式计算均衡化的灰度值
-
for j = 1:256
-
if a(j) > 0
-
b(j)=round(255*(a(j)),1);
-
end
-
end
-
-
%映射
-
for i = 1:R
-
for j = 1:C
-
I(i,j) = b(I(i,j)+1);
-
end
-
end
-
%查看均衡化后矩阵最大最小值
-
%Min2=min(min(I))%返回每一列最小的值后再取最小值
-
%Max2=max(max(I))
-
hist_img = I;
-
figure;
-
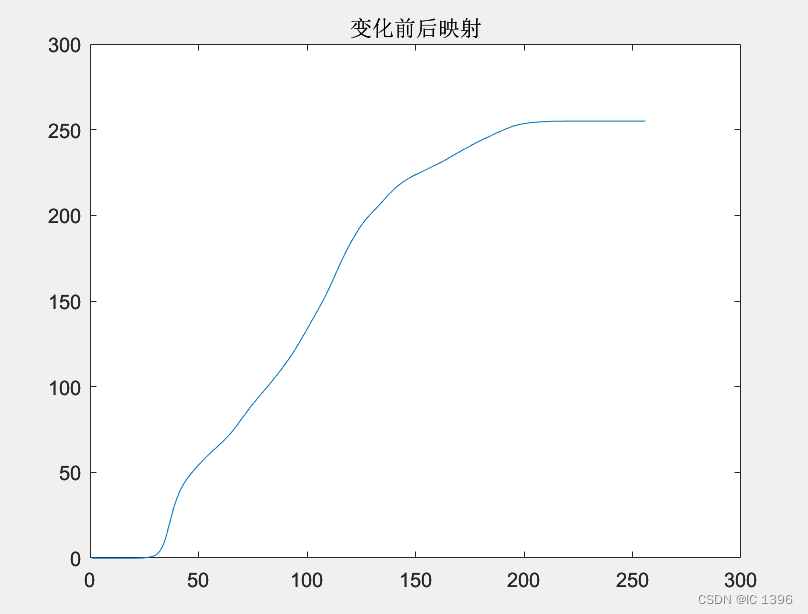
plot(b)
-
title(‘变化前后映射’)
-
-
end


2、直方图规定化
直方图规定化是一种图像处理技术,主要目的是将两幅图像的像素值分布调整到相似的范围,从而使它们在视觉上更加一致。其使用了一些数学统计的方法,将待处理图像的像素值映射到目标图像的像素值范围内。
直方图规定化的处理方法包括以下步骤:

直方图规定化被广泛应用于图像处理和计算机视觉领域,例如在图像匹配、图像拼接、图像增强等方面都有应用。
(1)使用histep函数实现图像均衡化
查看“使用histep函数实现图像均衡化”
(2)使用自行编写的规定化函数实现图像规定化
①实现一图像到另一图像规定化
-
%%
-
% 输入两幅图像实现规定化
-
clc;
-
Image1=imread(strip(input(‘请输入原图路径(图片右键复制文件地址即可):’,’s’),'”‘)); %读取图像
-
%判断是否转换为灰度值
-
while 1
-
str=input(‘是否需要转换为灰度图片(Y/N):’,’s’);
-
if str==’Y’
-
Image1=rgb2gray(Image1);
-
break
-
elseif str==’N’
-
break
-
else
-
disp(‘输入错误,请重新输入’)
-
end
-
end
-
-
Image2=imread(strip(input(‘请输入规定化路径(图片右键复制文件地址即可):’,’s’),'”‘)); %读取图像
-
-
result1 = prescriptive(Image1,Image2);%调用函数规定化
-
-
Hgram1 = imhist(Image1);%内置均衡化
-
Hgram2 = imhist(Image2);
-
result2 = histeq(Image1,Hgram2);
-
%result2 = histeq(Image1);
-
-
figure,
-
subplot(231),imshow(Image1),title(‘原图’);
-
subplot(234),imhist(Image1),title(‘原图直方图’);
-
subplot(232),imshow(result1),title(‘自行编写直方图规定化’);
-
subplot(235),imhist(result1),title(‘自行编写规定化直方图’);
-
subplot(233),imshow(result2),title(‘内置直方图规定化’);
-
subplot(236),imhist(result2),title(‘使用内置规定化直方图’);
-
-
%%
-
%函数部分——规定化函数
-
function prescribed_picture=prescriptive(I,J)
-
[R1, C1] = size(I);%获取图片行列像素点个数
-
img_size1 = R1*C1;%得总像素点
-
c1 = zeros(1,256);%返回1*256一维数组,元素均为0,用于统计每个灰度值像素的个数
-
b1= c1;%存档,用于转化前后的对照表
-
-
[R2, C2] = size(J);%获取图片行列像素点个数
-
img_size2 = R2*C2;%得总像素点
-
c2 = zeros(1,256);%返回1*256一维数组,元素均为0,用于统计每个灰度值像素的个数
-
%b2= c2;%存档,用于转化前后的对照表
-
-
temp1 = I(:);
-
temp1 = sort(temp1);%像素点灰度值排序
-
-
temp2 = J(:);
-
temp2 = sort(temp2);%像素点灰度值排序
-
-
-
for i = 1:img_size1 %遍历全部像素点
-
c1(temp1(i)+1) = c1(temp1(i)+1)+1; %索引c中对应的temp(i)+1位加1,temp为灰度值
-
end
-
-
for i = 1:img_size2 %遍历全部像素点
-
c2(temp2(i)+1) = c2(temp2(i)+1)+1; %索引c中对应的temp(i)+1位加1,temp为灰度值
-
end
-
-
-
a1 = c1./img_size1;
-
c1=a1;
-
a2 = c2./img_size2;
-
c2=a2;
-
for i = 2:256 %求和,得到累积分布函数
-
a1(i) = (c1(i) + a1(i-1));
-
a2(i) = (c2(i) + a2(i-1));
-
end
-
-
shine_upon=1;
-
proximit=256;
-
%计算规定化的灰度值
-
for j = 1:256
-
for i = 1:256
-
if shine_upon>abs((a1(j)-a2(i)))
-
shine_upon=abs((a1(j)-a2(i)));
-
proximit=i;
-
end
-
end
-
shine_upon=1;
-
%b1(j)=a2(proximit);
-
%b1(proximit)=b1(proximit)+a1(j);
-
b1(j)=proximit;
-
end
-
-
for i = 1:R1
-
for j = 1:C1
-
I(i,j) = b1(I(i,j)+1);
-
end
-
end
-
% Min2=min(min(I))%返回每一列最小的值后再取最小值
-
% Max2=max(max(I))
-
prescribed_picture = I;
-
figure;
-
plot(b1)
-
title(‘变化前后映射’)
-
end

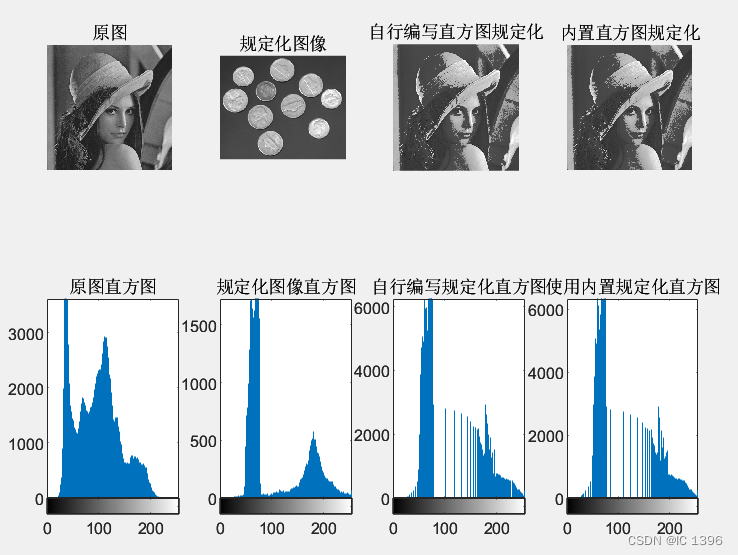
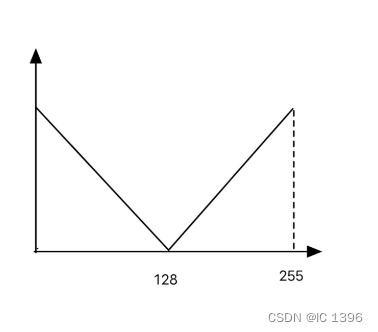
②将图像向一下直方图规定化
-
%%
-
%特定规定化直方图
-
clc;
-
Image1=imread(strip(input(‘请输入照片路径(图片右键复制文件地址即可):’,’s’),'”‘)); %读取图像
-
%判断是否转换为灰度图片
-
while 1
-
str=input(‘是否需要转换为灰度图片(Y/N):’,’s’);
-
if str==’Y’
-
Image1=rgb2gray(Image1);
-
break
-
elseif str==’N’
-
break
-
else
-
disp(‘输入错误,请重新输入’)
-
end
-
end
-
-
[result1,shine_upon,cumulative,prescriptive_diagram] = prescriptive2(Image1);%调用函数规定化
-
-
result2 = histeq(Image1,Hgram2);
-
-
figure,
-
subplot(231),imshow(Image1),title(‘原图’);
-
subplot(234),imhist(Image1),title(‘原图直方图’);
-
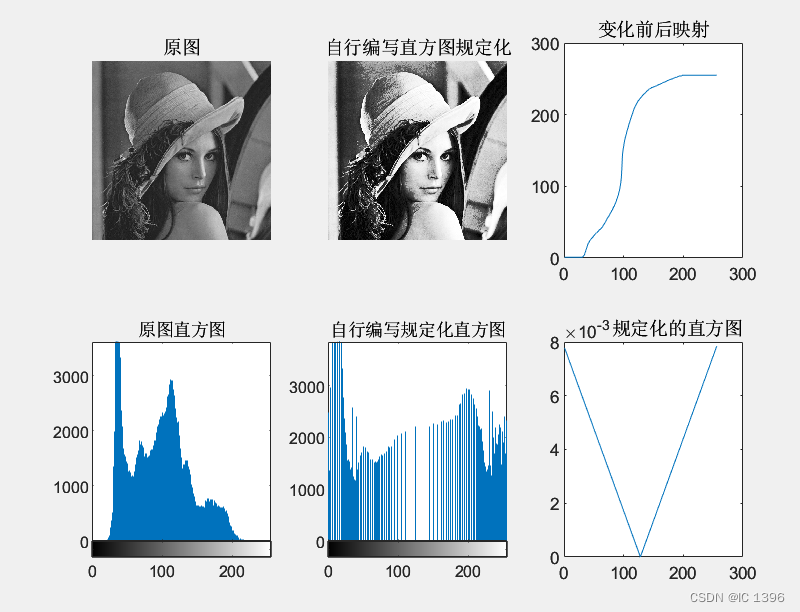
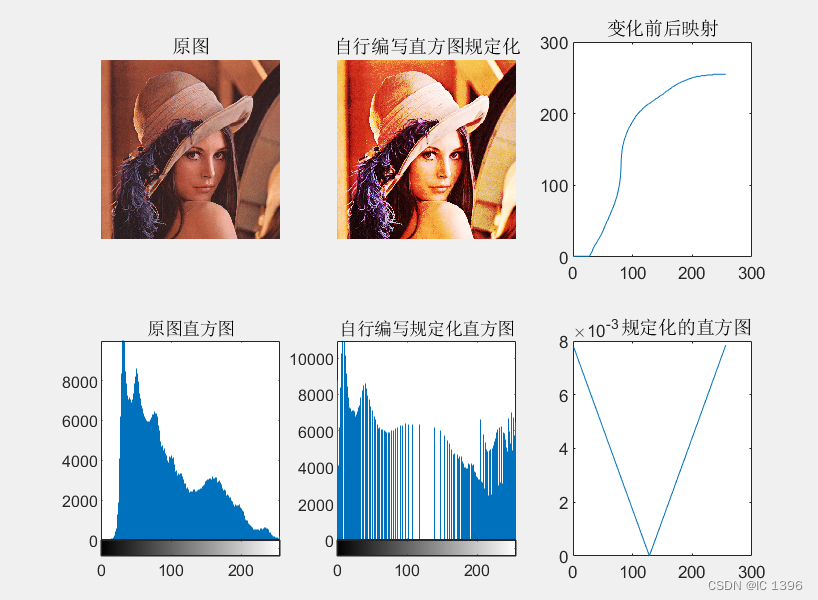
subplot(232),imshow(result1),title(‘自行编写直方图规定化’);
-
subplot(235),imhist(result1),title(‘自行编写规定化直方图’);
-
subplot(233),plot(shine_upon),title(‘变化前后映射’)
-
subplot(236),plot(prescriptive_diagram),title(‘ 规定化的直方图’)
-
-
%%
-
%函数部分-规定化函数(仅能规划到特定直方图)
-
function [prescribed_picture,b1,test2,test]=prescriptive2(I)
-
[R1, C1] = size(I);%获取图片行列像素点个数
-
img_size1 = R1*C1;%得总像素点
-
c1 = zeros(1,256);%返回1*256一维数组,元素均为0,用于统计每个灰度值像素的个数
-
b1= c1;%存档,用于转化前后的对照表
-
-
pixels = I(:);
-
pixels = sort(pixels);%像素点灰度值排序
-
-
for i = 1:img_size1 %遍历全部像素点
-
c1(pixels(i)+1) = c1(pixels(i)+1)+1; %索引c中对应的temp(i)+1位加1,temp为灰度值
-
end
-
-
a1 = c1./img_size1;%原始图像直方图
-
c1=a1;%存档用于累加
-
-
%规定化直方图编写
-
Max=2/255;%直方图峰值
-
%通过分段函数test(i)=a*i+Max i=1:128; test(i)=-a*i-Max i=128:256获得特定直方图
-
a=-Max/128;
-
test = zeros(1,256);
-
for i =1:128
-
test(i)=a*i+Max;
-
end
-
for i=128:256
-
test(i)=-a*i-Max;
-
end
-
-
test2=test;%存档用于累加
-
-
for i = 2:256 %求和,得到累积分布函数
-
a1(i) = (c1(i) + a1(i-1));
-
test2(i)=(test(i) + test2(i-1));
-
end
-
-
shine_upon=1;
-
proximit=256;
-
%计算规定化的灰度值
-
for j = 1:256
-
for i = 1:256
-
if shine_upon>abs((a1(j)-test2(i)))
-
shine_upon=abs((a1(j)-test2(i)));
-
proximit=i;
-
end
-
end
-
shine_upon=1;
-
%b1(j)=a2(proximit);
-
%b1(proximit)=b1(proximit)+a1(j);
-
b1(j)=proximit;%灰度级映射
-
end
-
%像素点映射
-
for i = 1:R1
-
for j = 1:C1
-
I(i,j) = b1(I(i,j)+1);
-
end
-
end
-
prescribed_picture = I;%返回映射图像
-
end

六、平滑滤波器
图像处理中的平滑滤波器是一种用于去除图像噪声和平滑图像的技术。平滑滤波器通常被设计为在局部像素区域内,即矩阵内对像素进行平均处理,以减少像素值之间的高频分量或图像中的病态噪声。
在图像处理中,常见的平滑滤波器包括:
①平均滤波器(average filter):将像素区域内的灰度平均值替换为当前像素的值。它可以减少噪声,但也可能导致图像变得模糊。
②中值滤波器(median filter):像素区域内的灰度值取中值代替,可以有效地去除脉冲噪声和非高斯分布的噪声,但是可能会导致图像边界和细节丢失。
③高斯滤波器(Gaussian filter):对周围像素进行加权平均,权重与像素之间的距离呈高斯分布,可以保留图像的细节和边缘特征。
④双边滤波器(bilateral filter):在相邻像素之间增加一个因素,使平滑程度与像素相似度成正比,可以有效地平滑图像并保留良好的边缘。
平滑滤波器的选择取决于所需的平滑度、速度、细节和边缘保留程度。在图像处理中,通常需要进行实验性比较以确定哪种滤波器最适合特定的应用。
-
%%
-
%课后作业二 1、使用滤波器
-
clc;
-
Image1=imread(strip(input(‘请输入lena路径(图片右键复制文件地址即可):’,’s’),'”‘)); %读取图像
-
Image3=imread(strip(input(‘请输入cameraman路径(图片右键复制文件地址即可):’,’s’),'”‘)); %读取图像
-
-
Image2=imnoise(Image1,”gaussian”,0.03);
-
%Image4=rgb2gray(Image2);
-
%平滑滤波器
-
%图像平滑
-
T1=1/9*ones(3);
-
T2=1/10*[1,1,1;
-
1,2,1;
-
1,1,1];
-
%图像增强
-
T3=[-1,-1,-1;
-
-1,9,-1;
-
-1,-1,-1];
-
T4=[0,-1,0;
-
-1,5,-1;
-
0,-1,0];
-
T5=[1,-2,1;
-
-2,5,-2;
-
1,-2,1];
-
%中值滤波
-
l=medfilt3(Image2);
-
%高斯滤波器
-
gaussian_filter1=fspecial(“gaussian”,8,5);
-
gaussian_filter2=fspecial(“gaussian”,8,3);
-
gaussian_filter3=fspecial(“gaussian”,8,1);
-
gaussian_filter4=fspecial(“gaussian”,8,0.1);
-
%分别使用平滑滤波器,高斯滤波器对图片卷积
-
T1_image=imfilter(Image2,T1,”replicate”,”full”,”conv”);
-
T2_image=imfilter(Image2,T2,”replicate”,”full”,”conv”);
-
T3_image=imfilter(Image3,T3,”replicate”,”full”,”conv”);
-
T4_image=imfilter(Image3,T4,”replicate”,”full”,”conv”);
-
T5_image=imfilter(Image3,T5,”replicate”,”full”,”conv”);
-
-
gaussian_Image1=imfilter(Image2,gaussian_filter1,”replicate”,”full”,”conv”);
-
gaussian_Image2=imfilter(Image2,gaussian_filter2,”replicate”,”full”,”conv”);
-
gaussian_Image3=imfilter(Image2,gaussian_filter3,”replicate”,”full”,”conv”);
-
gaussian_Image4=imfilter(Image2,gaussian_filter4,”replicate”,”full”,”conv”);
-
%平滑滤波图像
-
figure,
-
subplot(221),imshow(Image1),title(‘原图’);
-
subplot(222),imshow(Image2),title(‘添加高斯噪声’);
-
subplot(223),imshow(T1_image),title(‘T1image’);
-
subplot(224),imshow(T2_image),title(‘T2image’);
-
%中值滤波图像
-
figure,
-
subplot(121),imshow(Image2),title(‘原图’);
-
subplot(122),imshow(l),title(‘中值滤波’);
-
%图像增强图像
-
figure,
-
subplot(221),imshow(Image3),title(‘原图’);
-
subplot(222),imshow(T3_image),title(‘T3image’);
-
subplot(223),imshow(T4_image),title(‘T4image’);
-
subplot(224),imshow(T5_image),title(‘T5image’);
-
%高斯滤波图像
-
figure,
-
subplot(231),imshow(Image1),title(‘原图’);
-
subplot(234),imshow(Image2),title(‘添加高斯噪声’);
-
subplot(232),imshow(gaussian_Image1),title(‘sigma=5’);
-
subplot(233),imshow(gaussian_Image2),title(‘sigma=3’);
-
subplot(235),imshow(gaussian_Image3),title(‘sigma=1’);
-
subplot(236),imshow(gaussian_Image4),title(‘sigma=0.1’);

1、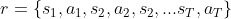
(1)图像平滑:
 图像平滑特点:卷积核元素和为1,使用图像平滑可以降噪,使得图片变得光滑
图像平滑特点:卷积核元素和为1,使用图像平滑可以降噪,使得图片变得光滑
(2)图像增强:

图像增强特点:卷积核元素和为0,上述图像使用了不同的卷积核,可以看出T3image的图像增强效果最好,但同时也带来噪点。图像增强增强了图像的对比度、亮度、色彩等,去除图像中的噪声、模糊和伪影等,从而使图像更加清晰、质量更好。
2、中值滤波

中值滤波特点:相比于线性滤波器,中值滤波器不会平滑图像的边缘使得图像更好地保留图像的边缘信息。
3、高斯滤波

高斯滤波特点:当sigma增加时,图片逐渐变得模糊,同时也变得光滑,边缘损失加剧。
七、Sobel算子、Prewitt算子、Roberts算子和LoG滤波器
1、Sobel算子
Sobel算子是一种常用的图像处理算子,用于在数字图像中进行边缘检测,其核心思想是通过计算像素值在两个方向上的梯度来检测图像中的边缘。Sobel算子是一种线性滤波器,通常与高斯滤波器一起使用。
Sobel算子可以检测垂直和水平方向上的变化,对于图像中的边缘或轮廓而言,常常表现为亮度变化或者颜色的变化。Sobel算子的运算方式类似于卷积,以3×3的矩阵为例,Sobel算子的核心矩阵如下:
-1 0 1
-2 0 2
-1 0 1
对于一幅灰度图像,可以利用Sobel算子分别对两个方向进行计算,以得到图像中所有的边缘信息,这些信息可以进一步用于图形分析、边缘检测、图像分割等诸多应用。
Sobel算子具有较强的抵抗噪声能力,它可以减少一些非边缘的噪声干扰,同时保持边缘的准确性,是一种常用的边缘检测算法。
2、Prewitt算子
Prewitt算子同Sobel算子一样是一种用于数字图像边缘检测的线性滤波器,它主要是用于检测图像中水平和垂直方向梯度的变化。Prewitt 算子与Sobel算子类似,它们的差别在于各自的卷积核。
Prewitt算子的卷积核可以表示为以下两个矩阵:
-1 0 1
-1 0 1
-1 0 1
或
-1 -1 -1
0 0 0
1 1 1
这两个卷积核分别对应了垂直和水平方向上的边缘信息。Prewitt算子也可分别用这两个核来检测图像中的水平和垂直边缘,它们的实际应用方式类似于Sobel算子。
与Sobel算子相比较,Prewitt算子还是有一些不同的。Prewitt算子相对来说计算速度较快,但它检测到的边缘可能并不如Sobel算子那样尖锐,而且不够稳健,对图像噪声抗干扰能力较低。因此在实际处理过程中,需要综合考虑应用情况和对算法性能要求等因素,选择合适的边缘检测算法。
3、Roberts算子
Roberts算子是图像处理中另一种常见的边缘检测算子,它也是一种线性滤波器,但与Sobel算子和Prewitt算子不同,Roberts算子通过在图片转换成的二维灰度图像中找出像素值的差异来检测边缘,该算法通常用于单色图像,即对于每个颜色通道都要进行边缘检测。
Roberts算子采用的是两个 2×2 的卷积核:
1 0
0 -1
这两个卷积核可用于分别对图像进行水平和垂直方向的卷积计算。在卷积过程中,原始图像中每一个像素点都与模板进行计算,最终得到的是图像中每一个像素点的边缘强度值。与Sobel算子类似,边缘检测结果是一张二值图像,黑色表示背景,白色表示图像中的边缘。
Roberts算子是一种简单直观的边缘检测算法,计算速度十分快速,尤其是在处理小型图像时。此外,该算法对于细节的反应很快,可以提供较为精确的边缘检测结果,但对于噪声敏感,存在一定的误检率问题。
4、LoG滤波器
LoG卷积滤波器,即Laplacian of Gaussian 滤波器,是在 拉普拉斯滤波Laaplacian Filter的基础上,把高斯滤波加入到其中,用于数字图像中的边缘、细节信息提取。相比于其他的图像滤波算法,LoG滤波算法可以实现多种图像特征的提取,如边缘、斑点和角点等。
LoG滤波器计算的是图像像素的二阶导数,以此来检测图像中的边缘信息和主峰点。通过在数字图像上使用LoG滤波器,可以得到黑色或白色的边缘,可以用于图像中的边缘检测。
5、几种算子的比较
Robert算子定位比较精确,但由于不包括平滑,所以对于噪声比较敏感;
Prewitt算子和Sobel算子都是一阶的微分算子,而前者是平均滤波,后者是加权平均滤波且检测的图像边缘可能大于2个像素。这两者对灰度渐变低噪声的图像有较好的检测效果,但是对于混合多复杂噪声的图像,处理效果就不理想了。;
LOG滤波器方法通过检测二阶导数过零点来判断边缘点。LOG滤波器中的a正比于低通滤波器的宽度,a越大,平滑作用越显著,去除噪声越好,但图像的细节也损失越大,边缘精度也就越低。所以在边缘定位精度和消除噪声级间存在着矛盾,应该根据具体问题对噪声水平和边缘点定位精度要求适当选取。
-
%%
-
%作业二 2、Sobel算子、Prewitt算子、Roberts算子和LoG算子
-
clc;
-
Image1=imread(strip(input(‘请输入lena路径(图片右键复制文件地址即可):’,’s’),'”‘)); %读取图像
-
Image2=imnoise(Image1,”gaussian”,0.03);
-
-
Image3=rgb2gray(Image1);
-
Image4=rgb2gray(Image2);
-
-
%Robert算子
-
Robert1=[ 0, 1;
-
-1, 0];
-
Robert2=[ 1, 0;
-
0,-1];
-
-
bw3=edge(Image3,”roberts”);
-
%Prewitt算子
-
Prewitt1=[-1, 0, 1;
-
-1, 0, 1;
-
-1, 0, 1];
-
-
Prewitt2=[-1,-1,-1;
-
0, 0, 0;
-
1, 1, 1];
-
%Sobel算子
-
Sobel1=[-1, 0, 1;
-
-2, 0, 2;
-
-1, 0, 1];
-
-
Sobel2=[-1,-2,-1;
-
0, 0, 0;
-
1, 2, 1];
-
%LoG算子
-
LoG=[ 0, 0,-1, 0, 0;
-
0,-1,-2,-1, 0;
-
-1,-2,16,-2,-1;
-
0,-1,-2,-1, 0;
-
0, 0,-1, 0, 0];
-
-
Robert1_Image1=imfilter(Image1,Robert1,”replicate”,”full”,”conv”);
-
Prewitt1_Image1=imfilter(Image1,Prewitt1,”replicate”,”full”,”conv”);
-
Sobel1_Image1=imfilter(Image1,Sobel1,”replicate”,”full”,”conv”);
-
Sobel2_Image1=imfilter(Image1,Sobel2,”replicate”,”full”,”conv”);
-
LoG_Image1=imfilter(Image1,LoG,”replicate”,”full”,”conv”);
-
-
Robert1_Image2=imfilter(Image2,Robert1,”replicate”,”full”,”conv”);
-
Prewitt1_Image2=imfilter(Image2,Prewitt1,”replicate”,”full”,”conv”);
-
Sobel1_Image2=imfilter(Image2,Sobel1,”replicate”,”full”,”conv”);
-
Sobel2_Image2=imfilter(Image2,Sobel2,”replicate”,”full”,”conv”);
-
LoG_Image2=imfilter(Image2,LoG,”replicate”,”full”,”conv”);
-
-
Robert1_Image3=imfilter(Image3,Robert1,”replicate”,”full”,”conv”);
-
Prewitt1_Image3=imfilter(Image3,Prewitt1,”replicate”,”full”,”conv”);
-
Sobel1_Image3=imfilter(Image3,Sobel1,”replicate”,”full”,”conv”);
-
Sobel2_Image3=imfilter(Image3,Sobel2,”replicate”,”full”,”conv”);
-
LoG_Image3=imfilter(Image3,LoG,”replicate”,”full”,”conv”);
-
-
Robert1_Image4=imfilter(Image4,Robert1,”replicate”,”full”,”conv”);
-
Prewitt1_Image4=imfilter(Image4,Prewitt1,”replicate”,”full”,”conv”);
-
Sobel1_Image4=imfilter(Image4,Sobel1,”replicate”,”full”,”conv”);
-
Sobel2_Image4=imfilter(Image4,Sobel2,”replicate”,”full”,”conv”);
-
LoG_Image4=imfilter(Image4,LoG,”replicate”,”full”,”conv”);
-
-
figure,
-
subplot(131),imshow(Image1),title(‘原图’);
-
subplot(132),imshow(bw3),title(‘原图’);
-
-
%显示卷积彩色图
-
figure,
-
subplot(231),imshow(Image1),title(‘原图’);
-
subplot(232),imshow(Robert1_Image1),title(‘Robert1_Image1’);
-
subplot(233),imshow(Prewitt1_Image1),title(‘Prewitt1_Image1’);
-
subplot(234),imshow(Sobel1_Image1),title(‘Sobel1_Image1’);
-
subplot(235),imshow(Sobel2_Image1),title(‘Sobel2_Image1’);
-
subplot(236),imshow(LoG_Image1),title(‘LoG_Image1’);
-
%显示卷积高斯彩色图
-
figure,
-
subplot(231),imshow(Image2),title(‘添加高斯噪声’);
-
subplot(232),imshow(Robert1_Image2),title(‘Robert1_Image2’);
-
subplot(233),imshow(Prewitt1_Image2),title(‘Prewitt1_Image2’);
-
subplot(234),imshow(Sobel1_Image2),title(‘Sobel1_Image2’);
-
subplot(235),imshow(Sobel2_Image2),title(‘Sobel2_Image2’);
-
subplot(236),imshow(LoG_Image2),title(‘LoG_Image2’);
-
%显示卷积灰度图
-
figure,
-
subplot(231),imshow(Image3),title(‘灰度图’);
-
subplot(232),imshow(Robert1_Image3),title(‘Robert1_Image3’);
-
subplot(233),imshow(Prewitt1_Image3),title(‘Prewitt1_Image3’);
-
subplot(234),imshow(Sobel1_Image3),title(‘Sobel1_Image3’);
-
subplot(235),imshow(Sobel2_Image3),title(‘Sobel2_Image3’);
-
subplot(236),imshow(LoG_Image3),title(‘LoG_Image3’);
-
%显示卷积高斯灰度图
-
figure,
-
subplot(231),imshow(Image4),title(‘灰度图添加高斯噪声’);
-
subplot(232),imshow(Robert1_Image4),title(‘Robert1_Image4’);
-
subplot(233),imshow(Prewitt1_Image4),title(‘Prewitt1_Image4’);
-
subplot(234),imshow(Sobel1_Image4),title(‘Sobel1_Image4’);
-
subplot(235),imshow(Sobel2_Image4),title(‘Sobel2_Image4’);
-
subplot(236),imshow(LoG_Image4),title(‘LoG_Image4’);

未添加高斯噪声:

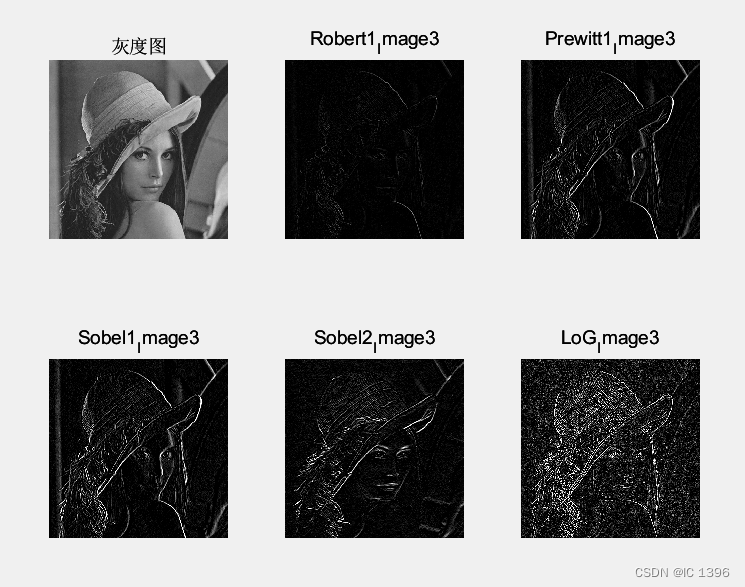
添加高斯噪声:
Sobel,Prewitt边缘检测较为准确,而Roberts提取边缘不太明显,但是提取的位置准确,没有将头发提取进去。而LoG提取边缘效果较强,帽子褶皱也被提取出来。对噪声比较敏感。在添加高斯噪声后,Sobel、Prewitt、LoG均被噪声干扰,而Roberts任然能够精确的提取边缘。此外Sobel1,Sobel2分别代表纵向和横向,检测效果也些许不同。
除了使用二维数组创建各类算子卷积核外,还可以使用edge生成相应的算子卷积核
-
bw1=edge(b,‘sobel’);%sobel算子
-
bw2=edge(b,‘prewitt’);%prewitt算子
-
bw3=edge(b,‘roberts’);%roberts算子
-
bw4=edge(b,‘log’); %log算子
-
bw5=edge(b,‘canny’);%canny算子
图片链接:百度网盘_提取码为MTLB
除了使用MATLAB进行图像处理外,python的cv2也可进行图像处理,感兴趣可以了解一下
MATLAB图像处理到此结束啦