大家好,今天和各位分享一下基于策略的深度强化学习方法,策略梯度法是对策略进行建模,然后通过梯度上升更新策略网络的参数。我们使用了 OpenAI 的 gym 库,基于策略梯度法完成了一个小游戏。完整代码可以从我的 GitHub 中获得:
https://github.com/LiSir-HIT/Reinforcement-Learning/tree/main/Model
1. 基于策略的深度强化学习
针对智能体在大规模离散动作下无法建模的难题,在基于值函数的深度强化学习中,利用神经网络对 Q 值函数近似估计,使深度学习与强化学习得到完美融合。
但是基于值函数的深度强化学习有一定的不足之处:
(1) 无法处理连续动作的任务。DQN 系列的算法可以较好地解决强化学习中大规模离散动作空间的任务,但在连续动作的任务中,难以实现利用深度神经网络对所有状态-动作的 Q 值函数近似表达。
(2) 无法处理环境中状态受到限制的问题。在基于值函数深度强化学习更新网络参数时,损失函数会依赖当前状态和下一个状态的值函数,当智能体在环境中观察的状态有限或建模受到限制时,就会导致实际环境中两个不同的状态有相同的价值函数,进而导致损失函数为零,出现梯度消失的问题。
(3) 智能体在环境中的探索性能较低。基于值函数的深度强化学习方法中,目标值都是从动作空间中选取一个最大价值的动作,导致智能体训练后的策略具有确定性,而面对一些需要随机策略进行探索的问题时,该方法就无法较好地解决。
由于基于值函数的深度强化学习存在上述的一些局限性,需要新的方法来解决这些问题,于是基于策略的深度强化学习被提出。该方法中将智能体当前的策略参数化,并且使用梯度的方法进行更新。
2. 策略梯度法
强化学习中策略梯度算法是对策略进行建模,然后通过梯度上升更新策略网络的参数。Policy Gradients 中无法使用策略的误差来构建损失函数,因为参数更新的目标是最大化累积奖励的期望值,所以策略更新的依据是某一动作对累积奖励的影响,即增加使累积回报变大的动作的概率,减弱使累积回报变小的动作的概率。
下图代表智能体在当前策略下,完成一个回合后构成的状态、动作序列 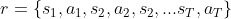 ,其中,Actor 是策略网络。每个回合结束后的累计回报为每个状态下采取的动作的奖励之和:
,其中,Actor 是策略网络。每个回合结束后的累计回报为每个状态下采取的动作的奖励之和:
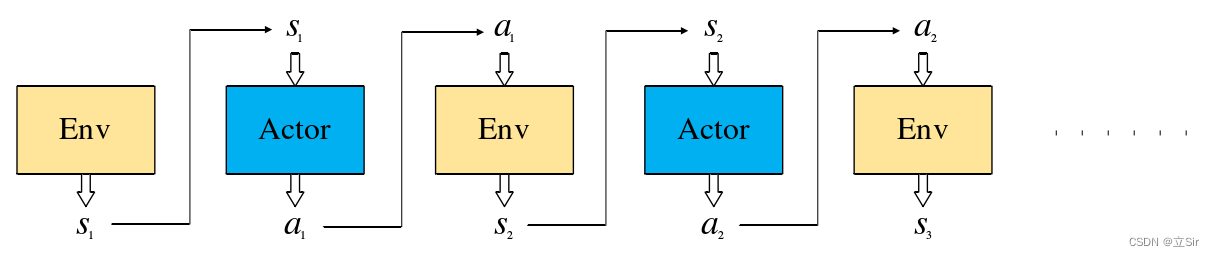
智能体在环境中执行策略 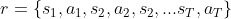 后状态转移概率:
后状态转移概率:
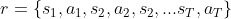
回合累计回报的期望:
![\bar{R}_\theta = \sum _{\tau } R(\tau ) P_\theta (\tau ) = E_{\tau \sim P_\theta (\tau )} [R(\tau )]](https://youzhan-cdn.oss-cn-beijing.aliyuncs.com/img/gif.latex.gif)
通过微分公式可以得到累计回报的梯度为:
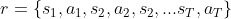
利用累计回报的梯度更新策略网络的参数:
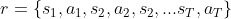
其中, 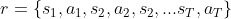 为梯度系数。通过上式的策略迭代可得,如果智能体在某个状态下采取的动作使累积回报增加,网络参数就会呈梯度上升趋势,该动作的概率就会增加,反之,梯度为下降趋势,减小该动作的概率。为了防止环境中所有的奖励都是正值,实现对于一些不好动作有一个负反馈,可以在总回报处减去一个基线。
为梯度系数。通过上式的策略迭代可得,如果智能体在某个状态下采取的动作使累积回报增加,网络参数就会呈梯度上升趋势,该动作的概率就会增加,反之,梯度为下降趋势,减小该动作的概率。为了防止环境中所有的奖励都是正值,实现对于一些不好动作有一个负反馈,可以在总回报处减去一个基线。
3. 代码实现
策略函数 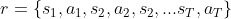 是一个概率密度函数,用于控制智能体的运动。
是一个概率密度函数,用于控制智能体的运动。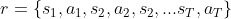 输入状态 s,输出每个动作 a 的概率分布。策略网络是指通过训练一个神经网络来近似策略函数。策略网络的参数
输入状态 s,输出每个动作 a 的概率分布。策略网络是指通过训练一个神经网络来近似策略函数。策略网络的参数 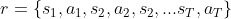 可通过策略梯度算法进行更新,从而实现对策略网络
可通过策略梯度算法进行更新,从而实现对策略网络 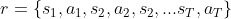 的训练。
的训练。
伪代码如下

模型构建部分代码如下:
-
# 基于策略的学习方法,用于数值连续的问题
-
import numpy as np
-
import torch
-
from torch import nn
-
from torch.nn import functional as F
-
-
# —————————————————– #
-
#(1)构建训练网络
-
# —————————————————– #
-
class Net(nn.Module):
-
def __init__(self, n_states, n_hiddens, n_actions):
-
super(Net, self).__init__()
-
# 只有一层隐含层的网络
-
self.fc1 = nn.Linear(n_states, n_hiddens)
-
self.fc2 = nn.Linear(n_hiddens, n_actions)
-
# 前向传播
-
def forward(self, x):
-
x = self.fc1(x) # [b, states]==>[b, n_hiddens]
-
x = F.relu(x)
-
x = self.fc2(x) # [b, n_hiddens]==>[b, n_actions]
-
# 对batch中的每一行样本计算softmax,q值越大,概率越大
-
x = F.softmax(x, dim=1) # [b, n_actions]==>[b, n_actions]
-
return x
-
-
# —————————————————– #
-
#(2)强化学习模型
-
# —————————————————– #
-
class PolicyGradient:
-
def __init__(self, n_states, n_hiddens, n_actions,
-
learning_rate, gamma):
-
# 属性分配
-
self.n_states = n_states # 状态数
-
self.n_hiddens = n_hiddens
-
self.n_actions = n_actions # 动作数
-
self.learning_rate = learning_rate # 衰减
-
self.gamma = gamma # 折扣因子
-
self._build_net() # 构建网络模型
-
-
# 网络构建
-
def _build_net(self):
-
# 网络实例化
-
self.policy_net = Net(self.n_states, self.n_hiddens, self.n_actions)
-
# 优化器
-
self.optimizer = torch.optim.Adam(self.policy_net.parameters(), lr=self.learning_rate)
-
-
# 动作选择,根据概率分布随机采样
-
def take_action(self, state): # 传入某个人的状态
-
# numpy[n_states]–>[1,n_states]–>tensor
-
state = torch.Tensor(state[np.newaxis, :])
-
# 获取每个人的各动作对应的概率[1,n_states]–>[1,n_actions]
-
probs = self.policy_net(state)
-
# 创建以probs为标准类型的数据分布
-
action_dist = torch.distributions.Categorical(probs)
-
# 以该概率分布随机抽样 [1,n_actions]–>[1] 每个状态取一组动作
-
action = action_dist.sample()
-
# 将tensor数据变成一个数 int
-
action = action.item()
-
return action
-
-
# 获取每个状态最大的state_value
-
def max_q_value(self, state):
-
# 维度变换[n_states]–>[1,n_states]
-
state = torch.tensor(state, dtype=torch.float).view(1,-1)
-
# 获取状态对应的每个动作的reward的最大值 [1,n_states]–>[1,n_actions]–>[1]–>float
-
max_q = self.policy_net(state).max().item()
-
return max_q
-
-
# 训练模型
-
def learn(self, transitions_dict): # 输入batch组状态[b,n_states]
-
# 取出该回合中所有的链信息
-
state_list = transitions_dict[‘states’]
-
action_list = transitions_dict[‘actions’]
-
reward_list = transitions_dict[‘rewards’]
-
-
G = 0 # 记录该条链的return
-
self.optimizer.zero_grad() # 优化器清0
-
# 梯度上升最大化目标函数
-
for i in reversed(range(len(reward_list))):
-
# 获取每一步的reward, float
-
reward = reward_list[i]
-
# 获取每一步的状态 [n_states]–>[1,n_states]
-
state = torch.tensor(state_list[i], dtype=torch.float).view(1,-1)
-
# 获取每一步的动作 [1]–>[1,1]
-
action = torch.tensor(action_list[i]).view(1,-1)
-
# 当前状态下的各个动作价值函数 [1,2]
-
q_value = self.policy_net(state)
-
# 获取已action对应的概率 [1,1]
-
log_prob = torch.log(q_value.gather(1, action))
-
# 计算当前状态的state_value = 及时奖励 + 下一时刻的state_value
-
G = reward + self.gamma * G
-
# 计算每一步的损失函数
-
loss = -log_prob * G
-
# 反向传播
-
loss.backward()
-
# 梯度下降
-
self.optimizer.step()

4. 实例演示
下面基于OpenAI 中的 gym 库,完成一个移动小车使得杆子竖直的游戏。状态states共包含 4 个,动作action有2个,向左和向右移动小车。迭代50回合,绘制每回合的 return 以及平均最大动作价值 q_max
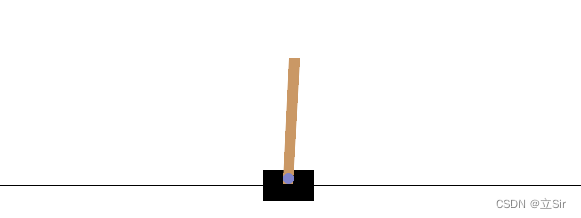
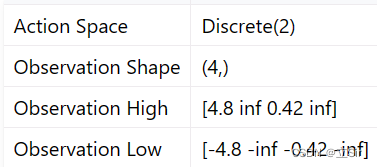
代码如下:
-
import gym
-
import numpy as np
-
import matplotlib.pyplot as plt
-
from RL_brain import PolicyGradient
-
-
# ——————————- #
-
# 模型参数设置
-
# ——————————- #
-
-
n_hiddens = 16 # 隐含层个数
-
learning_rate = 2e-3 # 学习率
-
gamma = 0.9 # 折扣因子
-
return_list = [] # 保存每回合的reward
-
max_q_value = 0 # 初始的动作价值函数
-
max_q_value_list = [] # 保存每一step的动作价值函数
-
-
# ——————————- #
-
#(1)加载环境
-
# ——————————- #
-
-
# 连续性动作
-
env = gym.make(“CartPole-v1″, render_mode=”human”)
-
n_states = env.observation_space.shape[0] # 状态数 4
-
n_actions = env.action_space.n # 动作数 2
-
-
# ——————————- #
-
#(2)模型实例化
-
# ——————————- #
-
-
agent = PolicyGradient(n_states=n_states, # 4
-
n_hiddens=n_hiddens, # 16
-
n_actions=n_actions, # 2
-
learning_rate=learning_rate, # 学习率
-
gamma=gamma) # 折扣因子
-
-
# ——————————- #
-
#(3)训练
-
# ——————————- #
-
-
for i in range(100): # 训练10回合
-
# 记录每个回合的return
-
episode_return = 0
-
# 存放状态
-
transition_dict = {
-
‘states’: [],
-
‘actions’: [],
-
‘next_states’: [],
-
‘rewards’: [],
-
‘dones’: [],
-
}
-
# 获取初始状态
-
state = env.reset()[0]
-
# 结束的标记
-
done = False
-
-
# 开始迭代
-
while not done:
-
# 动作选择
-
action = agent.take_action(state) # 对某一状态采取动作
-
# 动作价值函数,曲线平滑
-
max_q_value = agent.max_q_value(state) * 0.005 + max_q_value * 0.995
-
# 保存每一step的动作价值函数
-
max_q_value_list.append(max_q_value)
-
# 环境更新
-
next_state, reward, done, _, _ = env.step(action)
-
# 保存每个回合的所有信息
-
transition_dict[‘states’].append(state)
-
transition_dict[‘actions’].append(action)
-
transition_dict[‘next_states’].append(next_state)
-
transition_dict[‘rewards’].append(reward)
-
transition_dict[‘dones’].append(done)
-
# 状态更新
-
state = next_state
-
# 记录每个回合的return
-
episode_return += reward
-
-
# 保存每个回合的return
-
return_list.append(episode_return)
-
# 一整个回合走完了再训练模型
-
agent.learn(transition_dict)
-
-
# 打印回合信息
-
print(f’iter:{i}, return:{np.mean(return_list[-10:])}’)
-
-
# 关闭动画
-
env.close()
-
-
# ————————————– #
-
# 绘图
-
# ————————————– #
-
-
plt.subplot(121)
-
plt.plot(return_list)
-
plt.title(‘return’)
-
plt.subplot(122)
-
plt.plot(max_q_value_list)
-
plt.title(‘max_q_value’)
-
plt.show()

左图代表每回合的return,右图为平均最大动作价值