文章目录

1.堆的基本概念
- 1. 概念
- 2.性质
- - 1.必须为完全二叉树
  - 2.满足大堆/小堆成立的条件
- 3.存储方式
- - 1.逻辑结构
  - 2.物理结构
- 4. 孩子与父亲之间下标的关系
2.堆的基本实现
- 1.push——插入
- - 1.代码
  - 2. 情况分析
  - - 情况1
    - 情况2
  - 3. 向上调整算法
  - - 1.过程分析
    - 2. 临界条件的判断
- 2. pop—— 删除
- - 1.代码
  - 2. 向下调整算法
  - - 1. 注意事项
    - 2. 临界条件
    - 3.TOPK问题
    - - 1.过程分析
- 3. create ——建堆
- - 1.向下调整算法的应用
- 4. top—— 取堆顶元素
- 5. size—— 数据个数
- 6. empty ——判空
- 7. TOPK问题的具体实现
完整代码
- - 1.heap.h
  - 2.heap.c
  - 3.test.c

1.堆的基本概念

1. 概念

如果有一个关键码的集合K = { ，，，…， }，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足： <= 且
<= ( >= 且 >= ) i = 0，1，
2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

2.性质

1.必须为完全二叉树

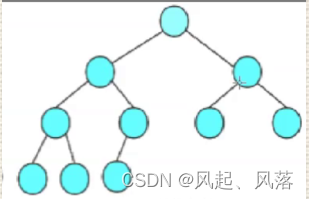
在这里插入图片描述

2.满足大堆/小堆成立的条件

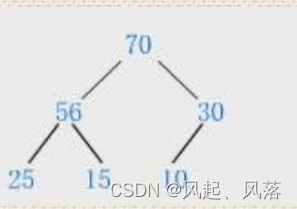
在这里插入图片描述

大堆：树中所有父亲节点都大于等于孩子节点

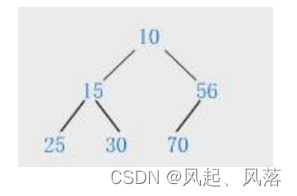
在这里插入图片描述

小堆：树中所有父亲节点都小于等于孩子节点

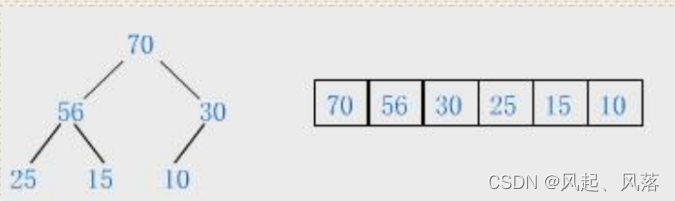
3.存储方式

1.逻辑结构

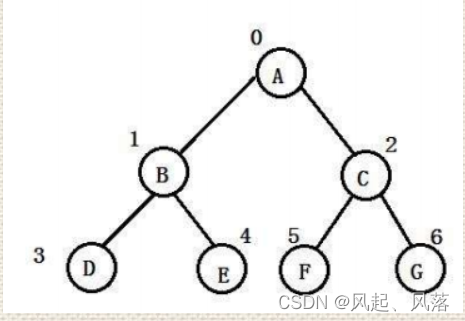
在这里插入图片描述

逻辑结构：我们想象出来的

2.物理结构

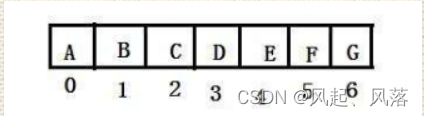
在这里插入图片描述

物理结构：实实在在在内存是如何存储的

4. 孩子与父亲之间下标的关系

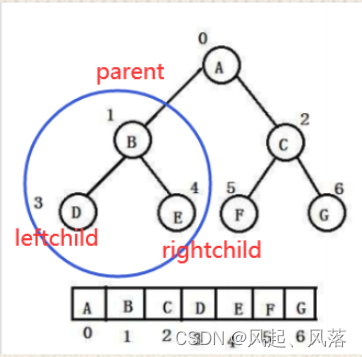
在这里插入图片描述

leftchild=parent*2+1
rightchild=parent*2+2
parent=(child-1)/2

这里child 可以是leftchild，也可以是rightchild，因为整数相除得到的结果也为整数

2.堆的基本实现

1.push——插入

1.代码

void adjustup(HPDatatype* a, int child)//向上调整算法
{
	int parent = (child - 1) / 2;
		while (child>0)
	{
		if (a[parent] >a[child])//以小堆为例
		{
		swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
        }
		else
		{
			break;
		}
	 }
}
void heappush(HP* php, HPDatatype x)//插入
{
	assert(php);
	if (php->capacity == php->size)//扩容
	{
		HPDatatype* ptr = (HPDatatype*)realloc(php->a, sizeof(HPDatatype)*php->capacity * 2);
		if (ptr != NULL)
		{
			php->a = ptr;
			php->capacity *= 2;
		}
	}
	php->a[php->size++] = x;//插入数据
	adjustup(php->a,php->size-1);  //向上调整

}

2. 情况分析

在这里插入图片描述

由图可知目前是一个小堆

情况1

在数组后插入 >=56 的数例如 100

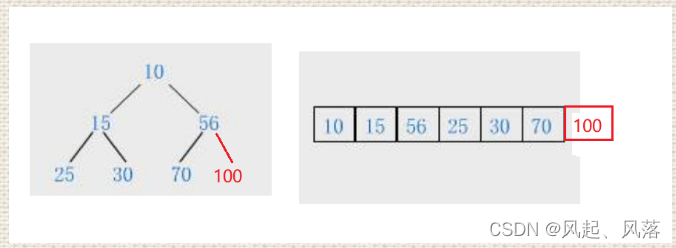
此时依旧为一个小堆，不需要调整，直接插入在数组尾部就可以了

情况2

在数组后插入<56的数例如 22
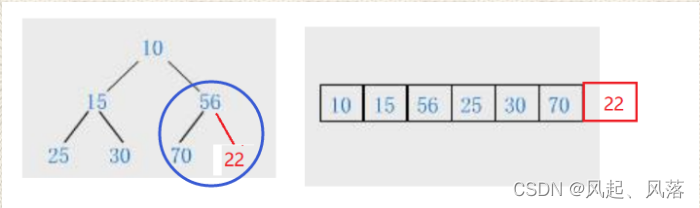
在圈中22比56小，所以不构成小堆，需要进行向上调整

3. 向上调整算法

1.过程分析

这里以小堆为例

在这里插入图片描述

我们要创建小堆，parent(56)>child(22)，所以要将两者值进行交换

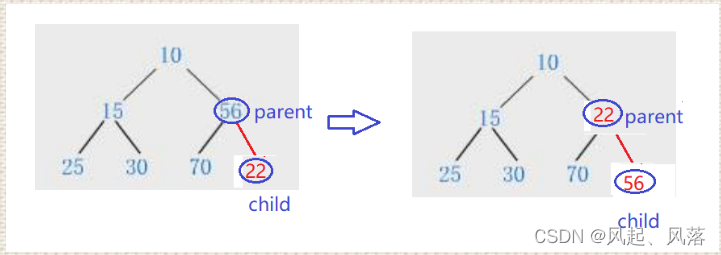
在这里插入图片描述

假设我们并不知道上面的数例如10 与新交换后的parent 22 的关系所以我们需要向上调整

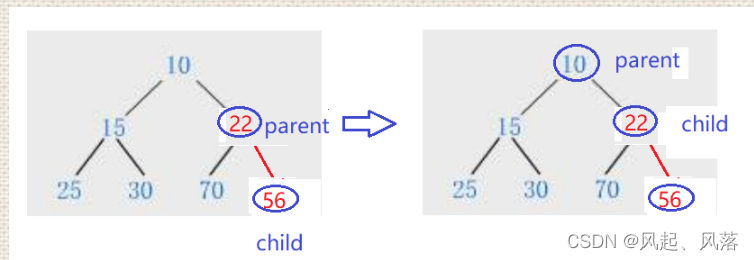
在这里插入图片描述

即将 parent的下标赋给 child ，即22成为新的child下标对应位置，10成为parent下标对应位置，此时因为10<22，所以走break不需要调整

2. 临界条件的判断

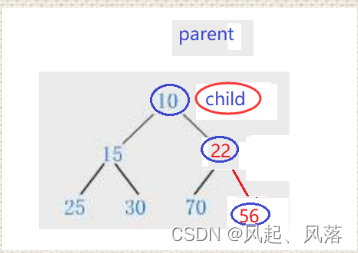
在这里插入图片描述

当child下标处于0时，parent下标已经越界没有比较的必要了，所以child>0
就为临界条件

2. pop—— 删除

1.代码

void adjustdown(HPDatatype* a, int parent,int size)//向下调整算法
{
	int child = parent * 2 + 1;//假设为左孩子
	while (child<size)
	{
		if (child+1<size&&a[child] < a[child + 1])//如果假设不成立，就为右孩子
		{
			child++;
		}
		if (a[parent] < a[child])//孩子大于父亲
		{
			swap(&a[parent], &a[child]);
			parent = child;
			child=parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void heappop(HP* php)//删除
{
	assert(php);
	assert(php->size > 0);
	swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	adjustdown(php->a,0,php->size);//向下调整算法
}

2. 向下调整算法

1. 注意事项

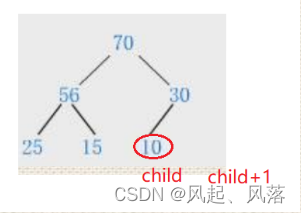
在这里插入图片描述

若右孩子所对应没有结点，a[child+1]就会越界访问，
所以需要加上限制条件： child+1<size

2. 临界条件

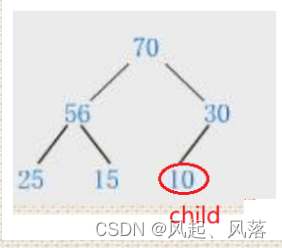
在这里插入图片描述

child作为下标存在，n为数据个数，child最多等于n-1

3.TOPK问题

N个数，找最大/最小的前k个

这里我们以大堆来举例寻找最大的前k个

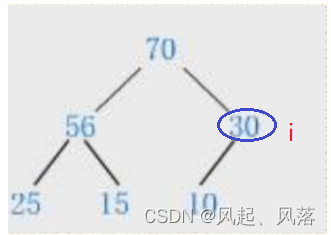
1.过程分析

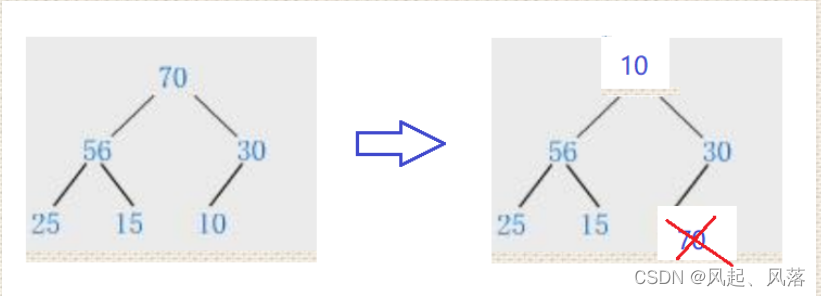
在这里插入图片描述

刚开始时，我们需要将首尾互换，并将此时的尾数据删除

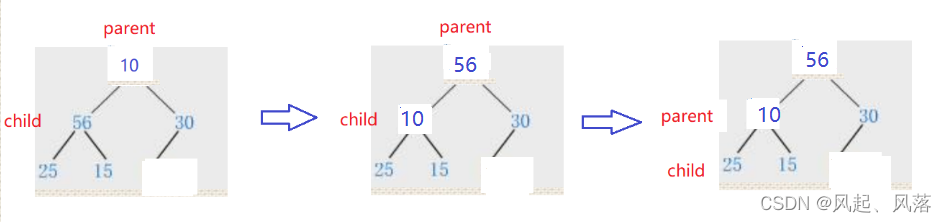
在这里插入图片描述

交换parent下标与child下标所对应的值，如图1 2
并将child的下标赋给parent 如图 2 3

3. create ——建堆

void heapcreate(HP* php, HPDatatype* a, int n)//建堆
{
	assert(php);
	php->a = (HPDatatype*)malloc(sizeof(HPDatatype) * n);
	if (php->a == NULL)
	{
		perror("mealloc fail");
		exit(-1);
	}
	memcpy(php->a, a,  sizeof(HPDatatype) * n);
	int i = 0;
	for (i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		adjustdown(php->a, i, n);
	}

1.向下调整算法的应用

在这里插入图片描述

我们想创建一个大堆，就必须使左子树是一个大堆及右子树是一个大堆
所以要从倒数第二层开始调整

4. top—— 取堆顶元素

HPDatatype heaptop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

5. size—— 数据个数

int heapsize(HP* php)//数据个数
{
	assert(php);
	assert(php->size > 0);
	return php->size;
}

6. empty ——判空

bool heapempty(HP* php)//判断是否为空
{
	assert(php);
	assert(php->size > 0);
	return php->size == 0;
}

7. TOPK问题的具体实现

#include "heap.h"
int main()
{
	HP php;
	heapinit(&php);
	int arr[] = {27,15,19,18,28,34,65,49,25,37};
	int sz = sizeof(arr) / sizeof(arr[0]);
	int i = 0;
	for (i = 0; i < sz; i++)
	{
		heappush(&php, arr[i]);
	}
	print(&php);
	int k = 5;//取前5个数
	while (k--)
	{
		printf("%d ", heaptop(&php));
		heappop(&php);
	}
	heapdestroy(&php);
	return 0;
}

在这里插入图片描述

完整代码

1.heap.h

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int  HPDatatype;
typedef struct Heap
{
	HPDatatype* a;
	int size;
	int capacity;
}HP;
void heapcreate(HP* php, HPDatatype *a, int size);
void heapinit(HP* php);//初始化
void heapdestroy(HP* php);//内存销毁
void heappush(HP* php,HPDatatype x);//插入
void heappop(HP* php);//删除
HPDatatype heaptop(HP* php);//堆顶数据
int heapsize(HP* php);//数据个数
bool heapempty(HP* php);//判断是否为空

2.heap.c

#include"heap.h"
void heapcreate(HP* php, HPDatatype *a, int n)//建堆
{
	assert(php);
	php->a = (HPDatatype*)malloc(sizeof(HPDatatype) * n);
	if (php->a == NULL)
	{
		perror("mealloc fail");
		exit(-1);
	}
	memcpy(php->a, a,  sizeof(HPDatatype) * n);
	php->size = n;
	php->capacity = n;
	int i = 0;
	for (i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		adjustdown(php->a, i, n);
	}

}



void  heapinit(HP* php)//初始化
{
	assert(php);
	php->a = (HP*)malloc(sizeof(php) *4);
	php->size = 0;
	php->capacity = 4;
}

void heapdestroy(HP* php)//内存销毁
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}
void swap(HPDatatype* s1, HPDatatype* s2)
{
	int tmp = 0;
	tmp = *s1;
	*s1 = *s2;
	*s2 = tmp;
}
//void adjustup(HPDatatype* a, int child)//向上调整算法
//{
//	int parent = (child - 1) / 2;
//	while (child>0)
//	{
//		if (a[parent] >a[child])//以小堆为例
//		{
//			swap(&a[parent], &a[child]);
//			child = parent;
//			parent = (child - 1) / 2;
//	    }
//		else
//		{
//			break;
//		}
//	}
//}
void adjustup(HPDatatype* a, int child)//向上调整算法
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] < a[child])//以大堆为例
		{
			swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void heappush(HP* php, HPDatatype x)//插入
{
	assert(php);
	if (php->capacity == php->size)//扩容
	{
		HPDatatype* ptr = (HPDatatype*)realloc(php->a, sizeof(HPDatatype)*php->capacity * 2);
		if (ptr != NULL)
		{
			php->a = ptr;
			php->capacity *= 2;
		}
	}
	php->a[php->size++] = x;//插入数据
	adjustup(php->a,php->size-1);  //向上调整

}
void adjustdown(HPDatatype* a, int parent,int size)//向下调整算法
{
	int child = parent * 2 + 1;//假设为左孩子
	while (child<size)
	{
		if (child+1<size&&a[child] < a[child + 1])//如果假设不成立，就为右孩子
		{
			child++;
		}
		if (a[parent] < a[child])//孩子大于父亲
		{
			swap(&a[parent], &a[child]);
			parent = child;
			child=parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void heappop(HP* php)//删除
{
	assert(php);
	assert(php->size > 0);
	swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	adjustdown(php->a,0,php->size);//向下调整算法
}
HPDatatype heaptop(HP* php)//取堆顶元素
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

void print(HP* php)
{
	int i = 0;
	for (i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}
bool heapempty(HP* php)//判断是否为空
{
	assert(php);
	assert(php->size > 0);
	return php->size == 0;
}

int heapsize(HP* php)//数据个数
{
	assert(php);
	assert(php->size > 0);
	return php->size;
}

#include "heap.h"
int main()
{
	HP php;
	heapinit(&php);
	int arr[] = {27,15,19,18,28,34,65,49,25,37};
	int sz = sizeof(arr) / sizeof(arr[0]);
	int i = 0;
	for (i = 0; i < sz; i++)
	{
		heappush(&php, arr[i]);
	}
	print(&php);
	int k = 5;
	while (k--)
	{
		printf("%d ", heaptop(&php));
		heappop(&php);
	}
	heapdestroy(&php);
	return 0;
}

3.test.c

#include "heap.h"
int main()
{
	HP php;
	int arr[] = { 27,15,19,18,28,34,65,49,25,37 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	int i = 0;
	heapcreate(&php, arr, sz);
	print(&php);
	/*for (i = 0; i < sz; i++)
	{
		heappush(&php, arr[i]);
	}
	print(&php);*/
	int k = 5;
	while (k--)
	{
		printf("%d ", heaptop(&php));
		heappop(&php);
	}
	heapdestroy(&php);
	return 0;
}

声明：本站所有资源，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。

文章目录

1.堆的基本概念

1. 概念

2.性质

1.必须为完全二叉树

2.满足大堆/小堆成立的条件

3.存储方式

1.逻辑结构

2.物理结构

4. 孩子与父亲之间下标的关系

2.堆的基本实现

1.push——插入

1.代码

2. 情况分析

情况1

情况2

3. 向上调整算法

1.过程分析

2. 临界条件的判断

2. pop—— 删除

1.代码

2. 向下调整算法

1. 注意事项

2. 临界条件

3.TOPK问题

1.过程分析

3. create ——建堆

1.向下调整算法的应用

4. top—— 取堆顶元素

5. size—— 数据个数

6. empty ——判空

7. TOPK问题的具体实现

完整代码

1.heap.h

2.heap.c

3.test.c

合作伙伴

我要赚钱

有站网，站长需要的精彩内容从这里开始

文章目录

1.堆的基本概念

1. 概念

2.性质

1.必须为完全二叉树

2.满足大堆/小堆成立的条件

3.存储方式

1.逻辑结构

2.物理结构

4. 孩子与父亲之间下标的关系

2.堆的基本实现

1.push——插入

1.代码

2. 情况分析

情况1

情况2

3. 向上调整算法

1.过程分析

2. 临界条件的判断

2. pop—— 删除

1.代码

2. 向下调整算法

1. 注意事项

2. 临界条件

3.TOPK问题

1.过程分析

3. create ——建堆

1.向下调整算法的应用

4. top—— 取堆顶元素

5. size—— 数据个数

6. empty ——判空

7. TOPK问题的具体实现

完整代码

1.heap.h

2.heap.c

3.test.c

相关文章